Inleiding tot Sorteeralgoritmen
Sorteren is een van de belangrijkste bewerkingen in informatica en data-analyse. Veel toepassingen, van zoekmachines tot databases en van sociale media tot e-commerceplatforms, maken gebruik van sorteeralgoritmen. Het efficiënt kunnen sorteren van gegevens kan systemen sneller maken, kosten besparen en de algehele gebruikservaring verbeteren.
Wat is Sorteren?
Sorteren betekent het rangschikken van een reeks elementen volgens een specifieke volgorde, zoals oplopend of aflopend. Het kan bijvoorbeeld gaan om een lijst van getallen, woorden of objecten.
In het dagelijks leven komen we vaak situaties tegen waarin sorteren nuttig of zelfs noodzakelijk is:
- Alfabetisch rangschikken van een lijst met namen: Bijvoorbeeld in een telefoonboek of adressenlijst.
- Producten rangschikken op prijs: Bijvoorbeeld wanneer een gebruiker zoekt naar de goedkoopste opties in een webshop.
- Chronologische volgorde van gebeurtenissen: Bijvoorbeeld wanneer je foto’s in een chronologische volgorde plaatst.
Voorbeelden van Scenario’s waarin Sorteren Belangrijk is
Hier zijn drie verschillende scenario’s waarin sorteren een belangrijke rol speelt:
- Sorteren van bestellingen op bezorgdatum: Bedrijven die pakketten verzenden, sorteren de bestellingen vaak op basis van de gewenste bezorgdatum. Dit helpt bij het prioriteren van leveringen en het plannen van de logistiek.
- Studenten ordenen op behaalde scores voor een examen: Een school kan bijvoorbeeld de resultaten van een examen sorteren om onderscheidingen toe te kennen aan de best presterende leerlingen.
- Sorteren van medische dossiers op urgentie: In ziekenhuizen kan het sorteren van dossiers op basis van urgentie helpen om patiënten die snelle zorg nodig hebben prioriteit te geven.
Tijdcomplexiteit en Big O Notatie
Wanneer we verschillende sorteeralgoritmen vergelijken, willen we weten welk algoritme het snelst werkt, vooral wanneer het aantal te sorteren elementen toeneemt. Hiervoor gebruiken we tijdscomplexiteit en de Big O-notatie.
Tijdscomplexiteit geeft aan hoe snel de uitvoeringstijd van een algoritme toeneemt naarmate de hoeveelheid data groeit. Dit helpt ons bepalen welk algoritme het meest efficiënt is voor een bepaalde taak.
Big O-notatie is een gestandaardiseerde manier om de tijdscomplexiteit van een algoritme te beschrijven. Het geeft de ergste gevalsscenario’s weer, zodat we weten hoe een algoritme presteert met grote hoeveelheden data.
Big O-notatie wordt vaak geschreven als O(f(n)), waarbij f(n) de tijdscomplexiteit voorstelt. Voor een simpele sorteermethode zoals Bubble Sort kan de tijdscomplexiteit O(n^2) zijn, wat betekent dat de uitvoeringstijd kwadratisch toeneemt naarmate de lijst groter wordt. Complexere algoritmen, zoals Merge Sort, hebben een lagere tijdscomplexiteit (O(n log n)) en zijn daarom sneller bij grotere datasets.
Selection Sort
Hoe werkt Selection Sort?
Het Selection Sort-algoritme sorteert een lijst door telkens het kleinste (of grootste) element uit het ongeordende deel van de lijst te selecteren en naar het begin te verplaatsen. Dit proces wordt herhaald voor elk element, waardoor de lijst uiteindelijk volledig gesorteerd wordt.
Het algoritme werkt als volgt:
- Zoek het kleinste element in de lijst.
- Wissel dit kleinste element met het eerste element.
- Zoek vervolgens het kleinste element in de resterende, nog niet gesorteerde, lijst en wissel dit met het volgende element in de rij.
- Herhaal dit proces totdat de hele lijst gesorteerd is.
Voorbeeld:
Bij een lijst zoals [29, 10, 14, 37, 13] zou Selection Sort eerst 10 vinden als het kleinste element en het naar voren wisselen met 29. Vervolgens wordt in het resterende deel [29, 14, 37, 13] het kleinste element 13 gevonden en verwisseld met 29, enzovoort.

Tijdcomplexiteit
De tijdcomplexiteit van Selection Sort is O(n²). Dit betekent dat de tijd die nodig is om de lijst te sorteren kwadratisch toeneemt met de grootte van de lijst. Selection Sort heeft een relatief lage efficiëntie bij grote lijsten, omdat het bij elk element steeds opnieuw de volledige (nog niet gesorteerde) lijst doorzoekt om het kleinste element te vinden.
Denk na: wat denk je over de efficiëntie van Selection Sort?
Vraag jezelf af: zou dit algoritme snel werken voor grote lijsten? Waarom wel of niet?
Implementatie: Stappenplan
Hier is een stappenplan voor de implementatie van Selection Sort. Gebruik dit plan om de code in Python te schrijven.
- Functie aanmaken: Schrijf een functie genaamd
selection_sortdie een lijst als parameter accepteert. - Doorloop de lijst: Gebruik een
for-lus om elk element in de lijst te doorlopen. - Zoek het minimum: Voor elk element, zoek het kleinste element in het resterende (nog niet gesorteerde) deel van de lijst.
- Wissel de elementen: Wissel het huidige element met het gevonden kleinste element.
- Herhaal: Herhaal dit proces voor elk element in de lijst totdat de hele lijst gesorteerd is.
Dit stappenplan helpt je bij het maken van een functionele implementatie van Selection Sort. Test je code met verschillende lijsten om te controleren of het algoritme correct werkt.
Bubble Sort
Hoe werkt Bubble Sort?
Bubble Sort werkt door telkens naast elkaar gelegen elementen in een lijst te vergelijken en te verwisselen als ze in de verkeerde volgorde staan. Het algoritme herhaalt dit proces totdat de volledige lijst gesorteerd is.
Stapsgewijze uitleg:
- Begin met het eerste element van de lijst.
- Vergelijk dit element met het volgende element.
- Als het eerste element groter is dan het volgende, verwissel de twee.
- Ga verder met het volgende paar, en herhaal de vergelijking en verwisseling waar nodig.
- Na één volledige doorloop (één “ronde”) staat het grootste element aan het einde van de lijst.
- Herhaal het proces voor de resterende elementen, waarbij je telkens één element minder vergelijkt, totdat de hele lijst gesorteerd is.
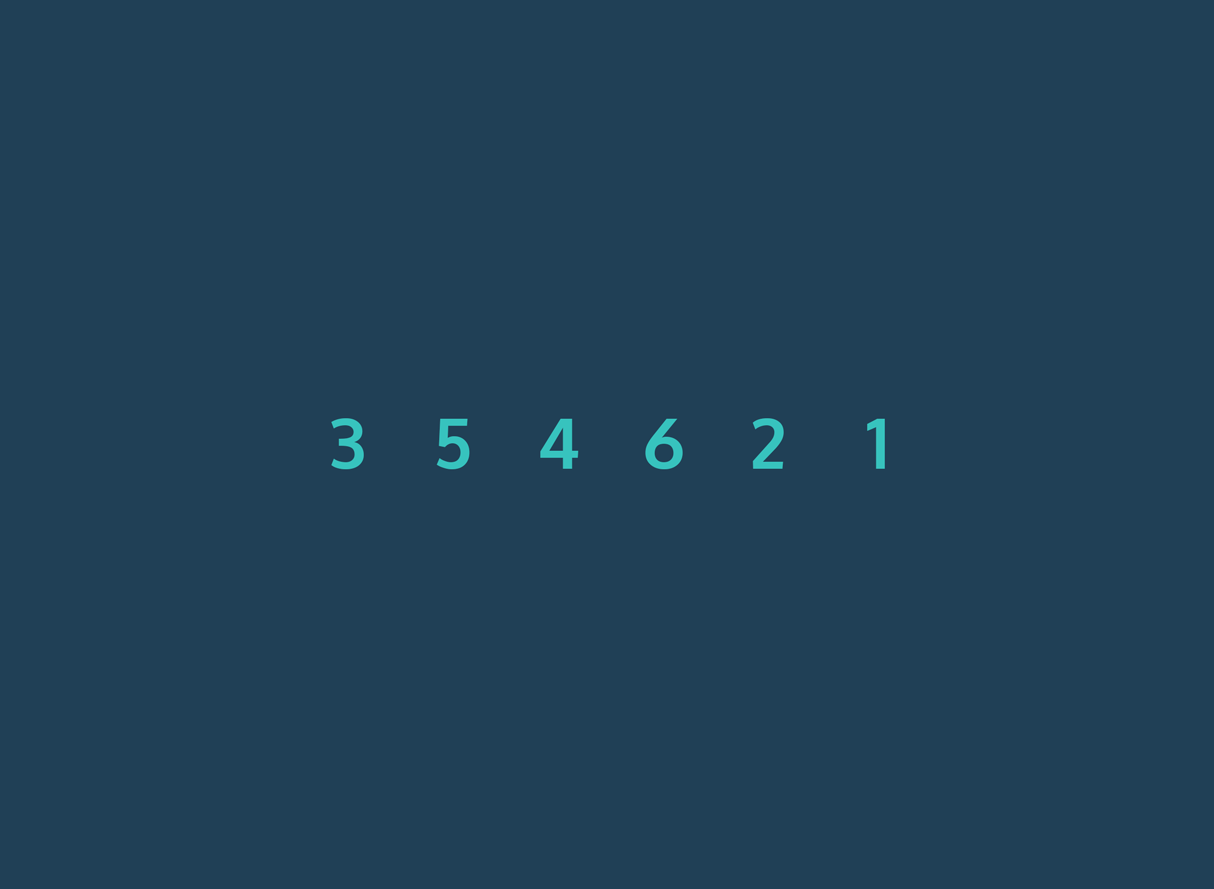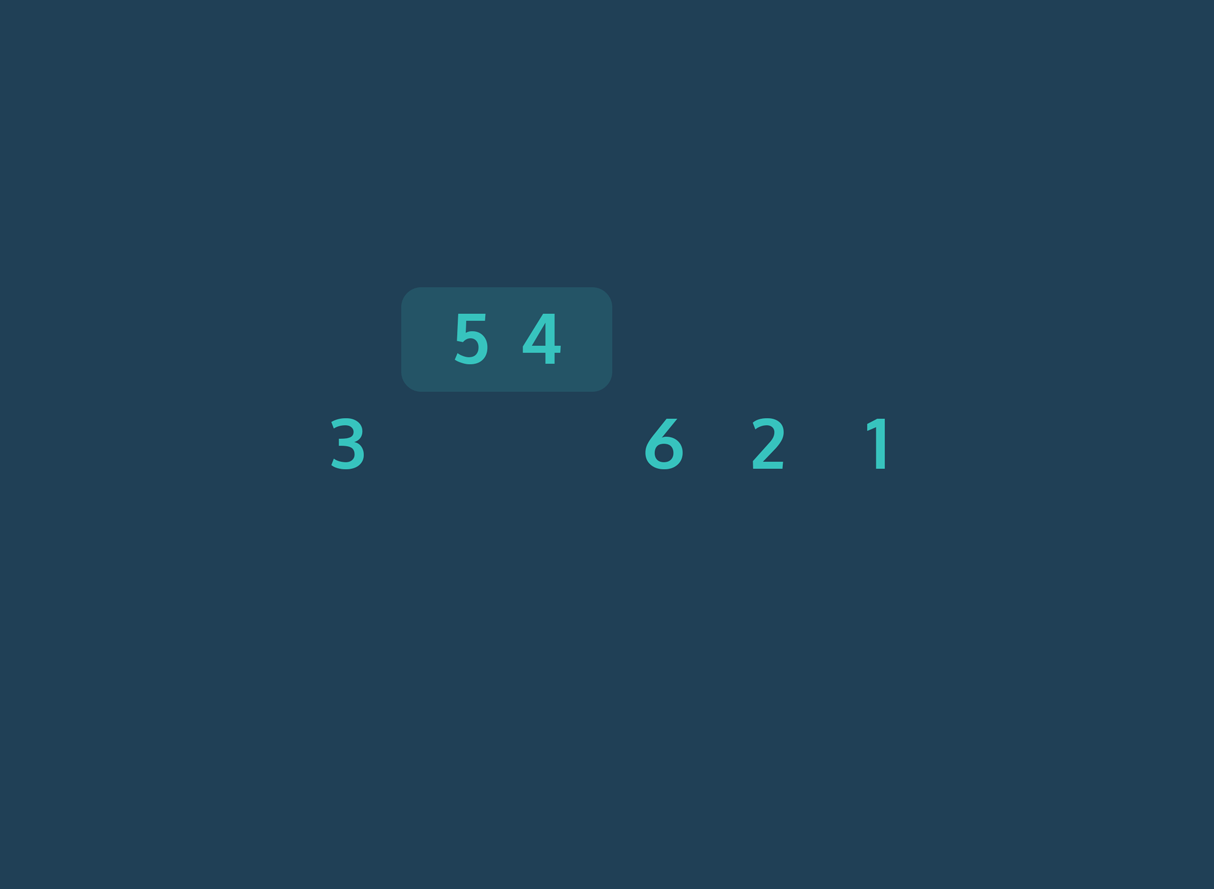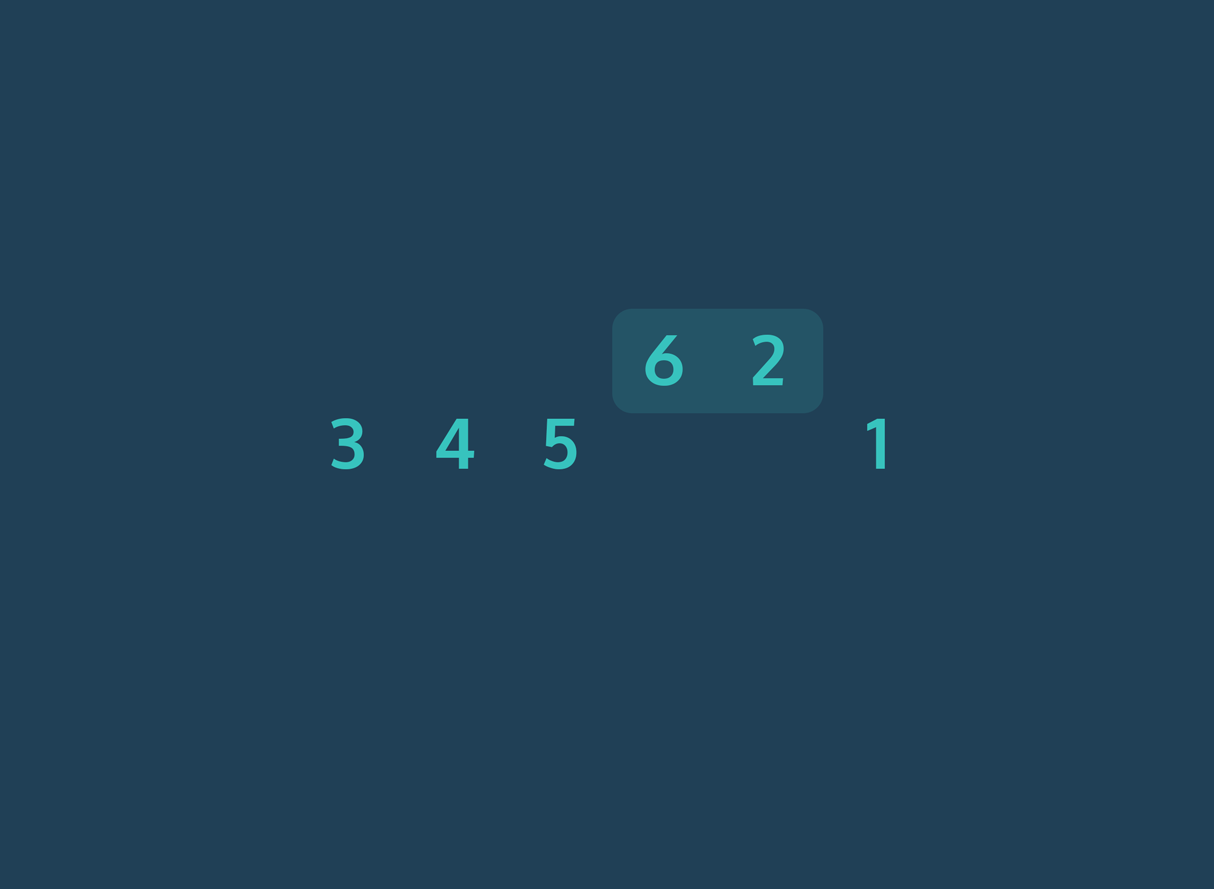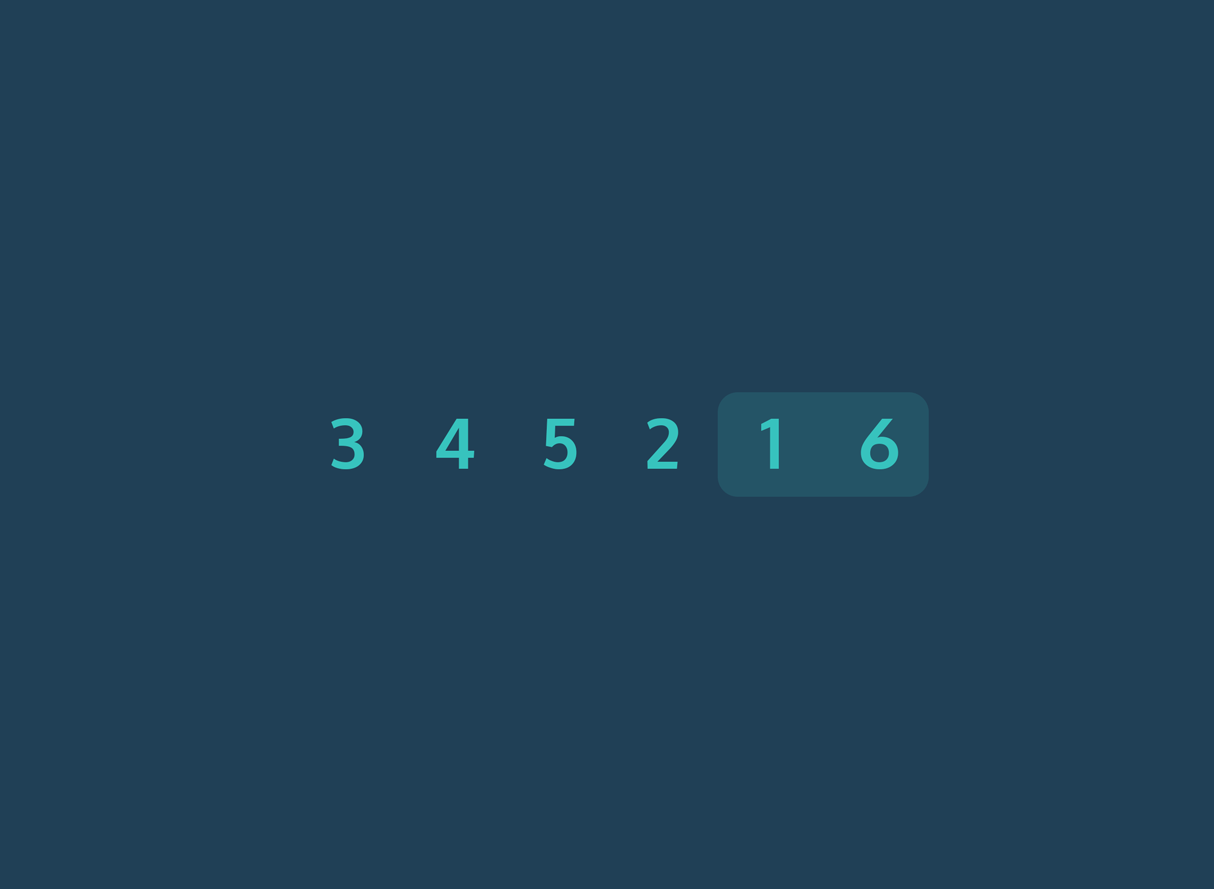
Efficiëntie en Complexiteit
Bubble Sort heeft een tijdscomplexiteit van O(n²). Dit betekent dat het algoritme relatief langzaam is bij grote lijsten, omdat de benodigde tijd exponentieel toeneemt met de grootte van de input. Bubble Sort is eenvoudig, maar vaak niet de meest efficiënte keuze voor grote lijsten.
Oefening: wat denk je over de efficiëntie van Bubble Sort? In welke situaties zou dit algoritme minder geschikt zijn?
Implementatie oefening: Stappenplan
Gebruik het volgende stappenplan om Bubble Sort te implementeren in Python.
- Schrijf een functie
bubble_sortdie een lijst als parameter accepteert. - Gebruik een
for-lus om de lijst meerdere keren door te lopen. - Vergelijk telkens twee naast elkaar gelegen elementen.
- Wissel de elementen als ze in de verkeerde volgorde staan.
- Herhaal deze stappen totdat de lijst volledig gesorteerd is.
Insertion Sort
Hoe werkt Insertion Sort?
Insertion Sort werkt door elk element op de juiste positie in een reeds gesorteerd deel van de lijst in te voegen. Dit betekent dat bij elke stap een element wordt vergeleken en verplaatst binnen het gesorteerde gedeelte van de lijst.
Stapsgewijze uitleg:
- Begin met het tweede element in de lijst (het eerste element vormt al een “gesorteerde” lijst van één element).
- Vergelijk dit element met de elementen ervoor.
- Verplaats het element naar de juiste positie binnen het gesorteerde deel.
- Ga verder met het volgende element en herhaal het proces, zodat elk element in het juiste deel van de lijst wordt ingevoegd.
- Herhaal deze stappen totdat de hele lijst gesorteerd is.

Efficiëntie en Complexiteit
Insertion Sort heeft ook een tijdscomplexiteit van O(n²) in het slechtste geval. Het algoritme is echter sneller dan Bubble Sort voor kleine of al deels gesorteerde lijsten, omdat er minder vergelijkingen en verplaatsingen nodig zijn in een bijna gesorteerde lijst.
Oefening: wat denk je over de efficiëntie van Insertion Sort? In welke situaties zou dit algoritme nuttiger zijn dan Bubble Sort?
Implementatie oefening: Stappenplan
Gebruik het volgende stappenplan om Insertion Sort te implementeren in Python.
- Schrijf een functie
insertion_sortdie een lijst als parameter accepteert. - Gebruik een
for-lus om door elk element van de lijst te gaan, beginnend vanaf het tweede element. - Vergelijk het element met de voorgaande elementen in het gesorteerde deel van de lijst.
- Verplaats het element naar de juiste positie binnen het gesorteerde deel.
- Herhaal deze stappen totdat de lijst volledig gesorteerd is.
Vergelijking tussen Bubble Sort en Insertion Sort
Bubble Sort en Insertion Sort zijn beide eenvoudige sorteeralgoritmen met een tijdscomplexiteit van O(n²), maar ze verschillen in hun aanpak en efficiëntie.
- Bubble Sort is minder efficiënt, omdat het altijd door de hele lijst moet gaan, ongeacht de initiële volgorde van de elementen. Dit maakt het minder geschikt voor grote of deels gesorteerde lijsten.
- Insertion Sort is efficiënter voor deels gesorteerde lijsten, omdat het elementen één voor één invoegt in het gesorteerde deel, wat leidt tot minder verplaatsingen en vergelijkingen in een bijna gesorteerde lijst.
Tip: Gebruik Insertion Sort voor kleine of bijna gesorteerde lijsten, en kies Bubble Sort alleen voor educatieve doeleinden of eenvoudige toepassingen.
Door de verschillen tussen deze algoritmen te begrijpen, kun je beter kiezen welk algoritme het meest geschikt is voor verschillende soorten gegevens en scenario’s.
Merge Sort – Een Eerste Complex Algoritme
In deze les leer je over Merge Sort, een krachtig sorteeralgoritme dat gebruikmaakt van het divide-and-conquer principe. Dit algoritme is efficiënter dan de eerder behandelde sorteeralgoritmen, vooral bij grote datasets.
Het Divide-and-Conquer-principe
Het divide-and-conquer principe is een strategie waarbij een probleem wordt opgesplitst in kleinere, eenvoudigere deelproblemen. Deze deelproblemen worden afzonderlijk opgelost en vervolgens gecombineerd om de uiteindelijke oplossing te vormen. Dit zorgt ervoor dat complexe problemen stap voor stap kunnen worden aangepakt.
Voorbeeld van divide-and-conquer: Stel je voor dat je een stapel kaarten hebt die je wilt sorteren. In plaats van de hele stapel tegelijk te sorteren, kun je deze in twee kleinere stapels verdelen en beide stapels afzonderlijk sorteren. Daarna kun je deze twee gesorteerde stapels combineren tot een volledige, gesorteerde stapel. Dit maakt het proces sneller en beter beheersbaar.
Hoe werkt Merge Sort?
Merge Sort maakt gebruik van het divide-and-conquer-principe om een lijst te sorteren. Het werkt als volgt:
- Verdelen: De lijst wordt steeds opgedeeld in twee helften totdat elke sublijst slechts één element bevat. Dit wordt gedaan omdat een enkele waarde per definitie al gesorteerd is.
- Oplossen: Zodra de lijst is verdeeld in individuele elementen, worden deze stap voor stap gecombineerd.
- Samenvoegen (Merge): Twee gesorteerde sublijsten worden gecombineerd tot een grotere gesorteerde lijst. Dit proces wordt herhaald totdat de volledige lijst weer één geheel vormt, maar dan gesorteerd.
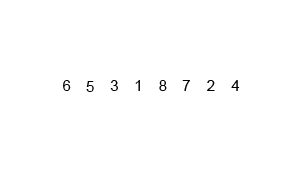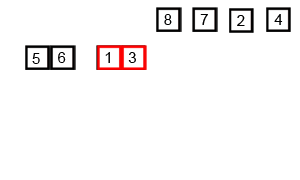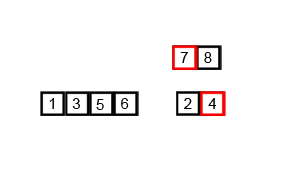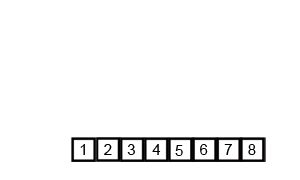
Voorbeeld:
Stel dat we de lijst [38, 27, 43, 3, 9, 82, 10] willen sorteren:
- De lijst wordt opgesplitst in twee helften:
[38, 27, 43, 3]en[9, 82, 10]. - Deze helften worden verder opgesplitst tot individuele elementen:
[38],[27],[43],[3],[9],[82],[10]. - Vervolgens worden de elementen samengevoegd en gesorteerd:
[27, 38],[3, 43],[9, 10],[82]. - Dit proces gaat door totdat alle elementen zijn gecombineerd tot de gesorteerde lijst
[3, 9, 10, 27, 38, 43, 82].
Voordelen van Merge Sort
Merge Sort biedt aanzienlijke voordelen ten opzichte van eenvoudigere sorteeralgoritmen zoals Bubble Sort en Insertion Sort:
- Efficiënt bij grote datasets: Doordat Merge Sort gebruikmaakt van het divide-and-conquer principe, kan het efficiënt omgaan met grote hoeveelheden data.
- Stabiel algoritme: Merge Sort behoudt de volgorde van gelijke elementen, wat handig kan zijn in specifieke toepassingen.
- Consistente prestaties: In tegenstelling tot andere algoritmen blijft de prestaties van Merge Sort stabiel, zelfs bij verschillende soorten data (bijv. gesorteerde, omgekeerde of willekeurige lijsten).
Tijdscomplexiteit en Efficiëntie
De tijdscomplexiteit van Merge Sort is O(n log n). Dit betekent dat de tijd die nodig is om een lijst te sorteren exponentieel minder toeneemt bij grotere datasets, vergeleken met algoritmen zoals Bubble Sort of Insertion Sort, die een complexiteit van O(n²) hebben.
Waarom is Merge Sort efficiënter voor grote datasets?
- In tegenstelling tot algoritmen met O(n²) complexiteit, die lineair door de lijst heen gaan voor elke vergelijking, verdeelt Merge Sort de lijst voortdurend in de helft, waardoor het aantal benodigde bewerkingen snel afneemt.
- Het
log n-gedeelte van de complexiteit verwijst naar het aantal keren dat de lijst kan worden verdeeld in kleinere stukken, terwijlnstaat voor de hoeveelheid data die gecombineerd moet worden tijdens het samenvoegen.
Voor grote datasets levert Merge Sort daarom aanzienlijke tijdswinst op, wat het een populaire keuze maakt voor situaties waarin efficiëntie essentieel is.
Protip: Voor kleine lijsten is Merge Sort misschien niet altijd de snelste keuze, maar voor grotere lijsten kan het enorm veel tijd besparen.
Quick Sort – Diepgaande Studie
In dit deel leer je over Quick Sort, een efficiënt sorteeralgoritme dat gebruikmaakt van het divide-and-conquer-principe, maar op een andere manier dan Merge Sort. Quick Sort is een krachtig algoritme dat vaak wordt gebruikt vanwege zijn snelheid en relatief lage geheugengebruik.
Wat is een Recursief Algoritme?
Een recursief algoritme is een algoritme dat zichzelf oproept om een deel van het probleem op te lossen. Het gebruikt een herhalend proces, waarbij het oorspronkelijke probleem steeds verder wordt opgesplitst tot er een eenvoudig, oplosbaar deelprobleem overblijft. Zodra alle deelproblemen zijn opgelost, worden de resultaten gecombineerd tot een complete oplossing.
Quick Sort is een voorbeeld van een recursief algoritme: het sorteert een lijst door de lijst steeds verder te verdelen en vervolgens te combineren.
Quick Sort en Divide-and-Conquer
Quick Sort maakt net als Merge Sort gebruik van het divide-and-conquer-principe, maar de aanpak verschilt. In plaats van een lijst eerst helemaal op te splitsen en daarna te combineren, kiest Quick Sort een pivot-element om de lijst direct in twee gesorteerde delen te verdelen.
Bij Quick Sort:
- Kies een pivot: Kies een element in de lijst als “pivot”.
- Verdeel de lijst: Schik alle elementen kleiner dan de pivot links en alle elementen groter dan de pivot rechts.
- Herhaal recursief: Pas Quick Sort recursief toe op de twee verkregen sublijsten (links en rechts van de pivot) totdat de volledige lijst gesorteerd is.
Hoe werkt Quick Sort en het Concept van Pivoting?
Quick Sort sorteert door steeds een pivot te kiezen en de lijst in twee delen te splitsen rond deze pivot. Het pivot-element fungeert als een scheidslijn: alle elementen links ervan zijn kleiner, en alle elementen rechts ervan zijn groter.
Stappen van Quick Sort:
- Kies een pivot-element in de lijst (bijvoorbeeld het eerste, laatste, of een willekeurig element).
- Verdeel de lijst in twee delen:
- Een deel met elementen die kleiner zijn dan de pivot.
- Een deel met elementen die groter zijn dan de pivot.
- Roep Quick Sort recursief aan voor elk deel (linker- en rechterkant van de pivot).
- Combineer de gesorteerde delen en de pivot om de volledige gesorteerde lijst te vormen.
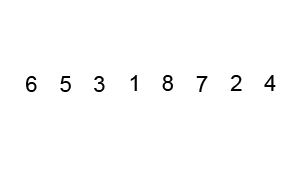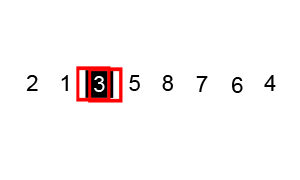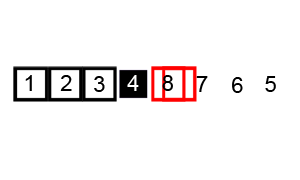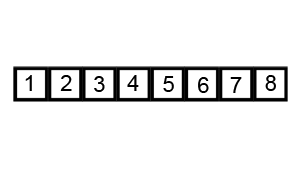
Het kiezen van de pivot kan op verschillende manieren gebeuren. Een willekeurige pivot zorgt meestal voor een betere verdeling van de elementen, wat de efficiëntie van het algoritme verhoogt.
Complexiteit en Efficiëntie van Quick Sort
De gemiddelde tijdscomplexiteit van Quick Sort is O(n log n), wat betekent dat het algoritme relatief snel werkt, zelfs voor grotere lijsten. Echter, in het slechtste geval kan de complexiteit oplopen tot O(n²), bijvoorbeeld wanneer de lijst al gesorteerd is en de pivot telkens een uiterste waarde kiest.
Een reeds gesorteerde of bijna gesorteerde lijst kan Quick Sort aanzienlijk vertragen als de pivot telkens het eerste of laatste element is. In dat geval ontstaat een onevenredig scheve verdeling, waardoor er meer stappen nodig zijn om te sorteren.
Waarom is een Willekeurige Pivot Belangrijk?
Een willekeurige pivot zorgt ervoor dat Quick Sort minder gevoelig is voor bepaalde lijstvolgordes, zoals een al gesorteerde lijst. Door een willekeurige pivot te kiezen, wordt de kans op een goede, evenwichtige splitsing vergroot, waardoor Quick Sort sneller werkt en de complexiteit in de praktijk dichter bij O(n log n) blijft.
Het gebruik van een willekeurige pivot maakt Quick Sort robuuster en verhoogt de kans dat het algoritme snel presteert, ongeacht de beginvolgorde van de lijst.
Quick Sort biedt een krachtig voorbeeld van hoe het divide-and-conquer-principe in sorteeralgoritmen kan worden toegepast. Hoewel het een complex algoritme is, zorgt de efficiëntie van Quick Sort ervoor dat het vaak wordt gebruikt voor toepassingen waarbij snelheid en lage geheugengebruik belangrijk zijn.
Experiment
In deze opdracht ga je experimenteren met de sorteeralgoritmen die we in eerdere lessen hebben behandeld. Je zult de prestaties van elk algoritme testen en de tijd meten die nodig is om lijsten van verschillende groottes te sorteren. Dit helpt om te begrijpen welk algoritme het meest efficiënt is voor verschillende datasetgroottes.
Doel van het Experiment
Het doel van dit experiment is om:
- De tijdsduur van verschillende sorteeralgoritmen te vergelijken.
- De efficiëntie van elk algoritme te begrijpen voor kleine en grote datasets.
- Inzicht te krijgen in wanneer je elk algoritme het beste kunt gebruiken.
Benodigde Stappen voor het Experiment
Volg de onderstaande stappen om het experiment uit te voeren. Werk in kleine groepen en noteer zorgvuldig de resultaten van jullie experimenten.
Stap 1: Lijsten met Willekeurige Getallen Maken
Voor deze opdracht heb je lijsten met willekeurige getallen nodig. Je kunt deze eenvoudig genereren in Python met de volgende code:
import random
# Lijst met 10 willekeurige getallen tussen 1 en 100
kleine_lijst = [random.randint(1, 100) for _ in range(10)]
# Lijst met 1000 willekeurige getallen tussen 1 en 10000
grote_lijst = [random.randint(1, 10000) for _ in range(1000)]
Gebruik een kleine lijst (10-20 elementen) en een grote lijst (1000-5000 elementen) voor je experimenten.
Stap 2: Tijd Meten
Om de tijd te meten die elk algoritme nodig heeft om een lijst te sorteren, gebruik je de time-module in Python. Hieronder vind je een voorbeeld van hoe je de tijd kunt meten:
import time
# Starttijd vastleggen
starttijd = time.time()
# Hier je sorteeralgoritme aanroepen, bijvoorbeeld bubble_sort(kleine_lijst)
# Eindtijd vastleggen
eindtijd = time.time()
# Tijdsduur berekenen
tijdsduur = eindtijd - starttijd
print("Tijd om te sorteren:", tijdsduur, "seconden")
Voeg deze tijdsmeting toe rond elk algoritme dat je test om de prestaties nauwkeurig te vergelijken.
Stap 3: Algoritmen Testen
Implementeer of gebruik bestaande implementaties van de volgende sorteeralgoritmen:
- Selection Sort
- Bubble Sort
- Insertion Sort
- Merge Sort
- Quick Sort
Voor elk algoritme:
- Voer het algoritme uit op de kleine lijst.
- Meet de tijd die het algoritme nodig heeft om de lijst te sorteren.
- Voer het algoritme uit op de grote lijst en meet opnieuw de tijd.
Zorg ervoor dat je de lijst opnieuw genereert voordat je elk algoritme test, zodat je telkens met een vergelijkbare, willekeurige lijst werkt.
Stap 4: Resultaten Noteren
Maak een tabel om je resultaten vast te leggen. Noteer voor elk algoritme de tijd die het nodig had om de kleine en grote lijst te sorteren. Je tabel kan er bijvoorbeeld zo uitzien:
| Algoritme | Kleine lijst (seconden) | Grote lijst (seconden) |
|---|---|---|
| Selection Sort | ||
| Bubble Sort | ||
| Insertion Sort | ||
| Merge Sort | ||
| Quick Sort |
Vul deze tabel in terwijl je de algoritmen test.
Stap 5: Analyse van de Resultaten
Bespreek binnen je groep de resultaten. Stel jezelf de volgende vragen:
- Welk algoritme was het snelst voor de kleine lijst? En voor de grote lijst?
- Zie je een groot verschil tussen de algoritmen met O(n²)-complexiteit (zoals Selection Sort, Bubble Sort en Insertion Sort) en de algoritmen met O(n log n)-complexiteit (zoals Merge Sort en Quick Sort)?
- Hoe beïnvloeden de grootte en samenstelling van de dataset de prestaties van elk algoritme?
Reflectie
Schrijf een korte samenvatting van je bevindingen. Welke algoritmen zou je kiezen voor kleine datasets, en welke voor grote datasets? Welke inzichten heb je opgedaan over de efficiëntie van sorteeralgoritmen?
Dit experiment helpt je om inzicht te krijgen in de prestaties van verschillende algoritmen en om weloverwogen keuzes te maken bij het sorteren van verschillende soorten data.
Toepassingen en Alternatieve Sorteeralgoritmen
In deze les verkennen we enkele alternatieve sorteeralgoritmen die anders werken dan de eerder behandelde vergelijkingsgebaseerde algoritmen, zoals Quick Sort en Merge Sort. Deze alternatieven, Counting Sort en Radix Sort, zijn voorbeelden van niet-vergelijkingsgebaseerde algoritmen en kunnen zeer efficiënt zijn in specifieke situaties.
Vergelijkingsgebaseerde vs. Niet-Vergelijkingsgebaseerde Sorteeralgoritmen
Vergelijkingsgebaseerde algoritmen sorteren gegevens door elementen met elkaar te vergelijken. Voorbeelden van deze algoritmen zijn Bubble Sort, Merge Sort, en Quick Sort. Bij deze algoritmen bepaalt het aantal vergelijkingen de efficiëntie, en ze hebben een theoretische ondergrens van O(n log n) voor hun complexiteit.
Niet-vergelijkingsgebaseerde algoritmen sorteren zonder elementen te vergelijken. In plaats daarvan maken ze gebruik van specifieke eigenschappen van de data, zoals de waarden of de cijfers in de getallen. Deze aanpak kan efficiënter zijn dan vergelijkingsgebaseerde algoritmen, vooral bij gegevens met een beperkt bereik of vaste structuur.
Voorbeeld: Niet-vergelijkingsgebaseerde algoritmen zijn handig voor het sorteren van getallen in een beperkt bereik, zoals leeftijden (bijv. 0-120) of postcodes.
Counting Sort
Counting Sort is een niet-vergelijkingsgebaseerd sorteeralgoritme dat goed werkt voor gehele getallen met een beperkt bereik. Het algoritme maakt een lijst van tellers voor elke mogelijke waarde binnen dat bereik en gebruikt die om de elementen te sorteren.
Voordelen van Counting Sort:
- Counting Sort is zeer efficiënt bij het sorteren van hele getallen binnen een beperkt bereik.
- Het algoritme heeft een tijdscomplexiteit van O(n + k), waarbij
nhet aantal elementen is enkhet bereik van de waarden. Dit kan sneller zijn dan vergelijkingsgebaseerde algoritmen alskklein is ten opzichte vann.
Voorbeeld: Stel dat we de lijst [4, 2, 2, 8, 3, 3, 1] willen sorteren met Counting Sort.
- Maak een lijst van tellers (
counts) voor alle mogelijke waarden in de lijst (bijvoorbeeld van 0 tot 8). - Tel hoe vaak elke waarde voorkomt:
[0, 1, 2, 2, 1, 0, 0, 0, 1]betekent dat er één 1, twee 2’s, één 3, etc. zijn. - Gebruik de
counts-lijst om de gesorteerde lijst op te bouwen door de waarden in volgorde toe te voegen:[1, 2, 2, 3, 3, 4, 8].
Counting Sort sorteert zonder elementvergelijkingen en is daarom sneller in situaties met een beperkt aantal unieke waarden.
Radix Sort
Radix Sort sorteert gegevens door de cijfers van elk element afzonderlijk te sorteren, beginnend met de minst significante cijfers (zoals eenheden) en verdergaand naar de meest significante cijfers (zoals duizenden). Radix Sort werkt goed voor getallen en strings met een vaste lengte.
Voordelen van Radix Sort:
- Radix Sort heeft een tijdscomplexiteit van O(d * (n + k)), waarbij
dhet aantal cijfers is enkhet bereik van elk cijfer (bijvoorbeeld 0-9 voor decimale getallen). - Het is zeer efficiënt voor het sorteren van grote aantallen gehele getallen of strings met een vaste lengte.
Voorbeeld van Radix Sort: Stel dat we de lijst [170, 45, 75, 90, 802, 24, 2, 66] willen sorteren met Radix Sort.
- Eerste stap (eenheden): Sorteer de lijst op de eenheden-cijfers. Resultaat:
[170, 90, 802, 2, 24, 45, 75, 66]. - Tweede stap (tientallen): Sorteer de lijst op de tientallen-cijfers. Resultaat:
[802, 2, 24, 45, 66, 170, 75, 90]. - Derde stap (honderdtallen): Sorteer de lijst op de honderdtallen-cijfers. Resultaat:
[2, 24, 45, 66, 75, 90, 170, 802].
Door de cijfers van minst naar meest significant te sorteren, bouwt Radix Sort een volledig gesorteerde lijst op.
Case Study Oefening
Voor deze oefening kies je één van de niet-vergelijkingsgebaseerde algoritmen, Counting Sort of Radix Sort, en pas je deze toe in een specifieke situatie. Volg de onderstaande stappen om je case study uit te voeren.
Stap 1: Dataset Kiezen
Kies een dataset die past bij het algoritme dat je hebt gekozen. Enkele voorbeelden:
- Voor Counting Sort: een lijst van leeftijden tussen 0 en 120 of een lijst van scores tussen 0 en 100.
- Voor Radix Sort: een lijst van postcodes of een reeks telefoonnummers.
Stap 2: Implementatie van het Algoritme
- Implementeer Counting Sort of Radix Sort in Python. Gebruik je eerdere implementaties of schrijf een nieuwe.
- Zorg ervoor dat je het algoritme toepast op de gekozen dataset en dat de stappen van het algoritme goed gevolgd worden.
Stap 3: Resultaten en Reflectie
- Noteer je resultaten, inclusief de gesorteerde lijst en de tijd die nodig was om de lijst te sorteren (optioneel).
- Reflecteer op de efficiëntie van het algoritme en op waarom dit algoritme geschikt was voor jouw dataset.
Schrijf een korte samenvatting van je case study en bespreek waarom je gekozen hebt voor Counting Sort of Radix Sort. Welke voordelen zag je in de toepassing van dit algoritme voor je dataset?
Met deze oefening leer je hoe je specifieke sorteeralgoritmen kunt toepassen op geschikte datasets en krijg je inzicht in de verschillende toepassingen en efficiëntie van niet-vergelijkingsgebaseerde sorteeralgoritmen.